Question

In Melanie's Styling Salon, the time to complete a simple haircut is normally distributed with a mean of 25 minutes and a standard deviation of 4 minutes. The slowest quartile of customers will require longer than how many minutes for a simple haircut?

(A) 3(n+1)/4 minutes
(B) 26 minutes
(C) 25.7 minutes
(D) 27.7 minutes

Answer 1

(D) 27.7 minutes

Explanation:

The slowest quartile starts at the 75th percentile:

The z-score for the 75th percentile is approximately 0.675. Z-score is given by:

`z=(x-\mu)/(\sigma) \\`

Where 'μ' is the population mean and 'σ' is the standard deviation

At the 75th percentile, the time for a haircut is:

`0.675=(x-25)/(4) \\\\x=0.675*4 +25\\x=27.7 \ minutes`

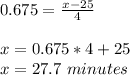
Therefore, the slowest quartile will require at least 27.7 minutes for a haircut.