Answer:
a)
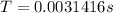
b)
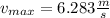
c)
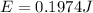
d)
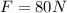
e)
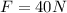
Step-by-step explanation:
1) Important concepts
Simple harmonic motion is defined as "the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law (F=-Kx). The motion experimented by the particle is sinusoidal in time and demonstrates a single resonant frequency".
2) Part a
The equation that describes the simple armonic motion is given by
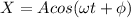 (1)
(1)
And taking the first and second derivate of the equation (1) we obtain the velocity and acceleration function respectively.
For the velocity:
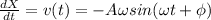 (2)
(2)
For the acceleration
 (3)
(3)
As we can see in equation (3) the acceleration would be maximum when the cosine term would be -1 and on this case:
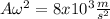
Since we know the amplitude A=0.002m we can solve for
 like this:
like this:

And we with this value we can find the period with the following formula
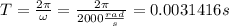
3) Part b
From equation (2) we see that the maximum velocity occurs when the sine function is euqal to -1 and on this case we have that:
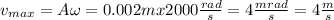
4) Part c
In order to find the total mechanical energy of the oscillator we can use this formula:

5) Part d
When we want to find the force from the 2nd Law of Newton we know that F=ma.
At the maximum displacement we know that X=A, and in order to that happens
 , and we also know that the maximum acceleration is given by::
, and we also know that the maximum acceleration is given by::
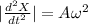
So then we have that:
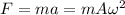
And since we have everything we can find the force
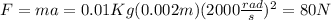
6) Part e
When the mass it's at the half of it's maximum displacement the term
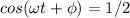 and on this case the acceleration would be given by;
and on this case the acceleration would be given by;

And the force would be given by:
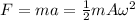
And replacing we have:
