Question

A 2.15g sample of benzene (C_6H_6) is burned in a bomb calorimeter, and the temperature rises from 22.46 degree C to 34.34 degree C. Calculate the heat capacity of the bomb calorimeter. Note the following thermochemical equation: C_6H_6(I) + 15/2 O_2 (g) rightarrow 6CO_2 (g) + 3H_2O (g) Delta H degree = -3267.5 kJ

Answer 1

The heat capacity of the bomb calorimeter is 7.58 J/°C.

Step-by-step explanation:

`C_6H_6(I) + (15)/(2) O_2 (g) \rightarrow 6CO_2 (g) + 3H_2O (g) ,\Delta H^o = -3267.5 kJ`

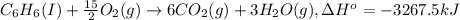
First, we will calculate energy released on combustion:

`\Delta H` = enthalpy change = -3267.5 kJ/mol

q = heat energy released

n = number of moles benzene=
`\frac{\text{Mass of benzene}}{\text{Molar mass of benzene}}=(2.15 g g)/(78 g /mol)=0.02756 mol`

`\Delta H=-(q)/(n)`

`q=\Delta H* n =-3267.5 kJ/mol* 0.02756 mol=-90.0657 kJ`

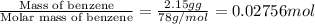
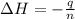
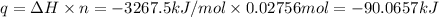
q = -90.0657 kJ = -90,065.7 J

Now we calculate the heat gained by the calorimeter let it be Q.

Q = -q= -(-90,065.7 J) = 90,065.7 J (conservation of energy)

`Q=c* (T_(final)-T_(initial))`

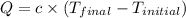
where,

Q = heat gained by calorimeter

c = specific heat capacity of calorimeter =?

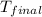`T_(final)` = final temperature =
`34.34^oC`

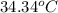
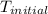`T_(initial)` = initial temperature =
`22.46^oC`

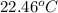
Now put all the given values in the above formula, we get:

`90,065.7 J=c* (34.34-22.46)^oC`

`c=(90,065.7 J)/((34.34-22.46)^oC)=7.58 J/^oC`

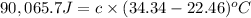
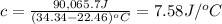
The heat capacity of the bomb calorimeter is 7.58 J/°C.