Question

A high-jumper, having just cleared the bar, lands on an air mattress and comes to rest. Had she landed directly on the hard ground, her stopping time would have been much shorter. Using the impulse-momentum theorem as your guide, determine which one of the following statements is correct.

a. the air mattress exerts the same impulse, but a greater net average force, on the high-jumper than does the hard groundb. the air mattress exerts a greater impulse, and a greater net average force, on the high-jumper than does the hard groundc. the air mattress exerts a smaller impulse, and a smaller net average force, on the high-jumper than does the hard groundd. the air mattress exerts a greater impulse, but a smaller net average force, on the high-jumper than does the hard grounde. the air mattress exerts the same impulse, but a smaller net avg force, on the hj than hg

Answer 1

e. the air mattress exerts the same impulse, but a smaller net avg force, on the high-jumper than hard-ground.

Step-by-step explanation:

This is according to the Newton's second law and energy conservation that the force exerted by the hard-ground is more than the force exerted by the mattress.

The hard ground stops the moving mass by its sudden reaction in the opposite direction of impact force whereas the mattress takes a longer time to stop the motion of same mass in a longer time leading to lesser average reaction force.

Mathematical expression for the Newton's second law of motion is given as:

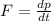`F=(dp)/(dt)` ............................................(1)

where:

dp = change in momentum

dt = time taken to change the momentum

We know, momentum:

`p=m.v`

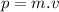
Now, equation (1) becomes:

`F=(d(m.v))/(dt)`

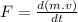
∵mass is constant at speeds v << c (speed of light)

`\therefore F=m.(dv)/(dt)`

and,
`(dv)/(dt) =a`

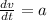
where: a = acceleration

`\Rightarrow F=m.a`

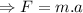
also

`F\propto (1)/(dt)`

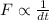
so, more the time, lesser the force.

& Impulse:

`I=F.dt`

`I=m.a.dt`

`I=m.(dv)/(dt).dt`

`I=m.dv=dp`

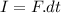
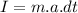
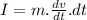
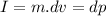
∵Initial velocity and final velocity(=0), of a certain mass is same irrespective of the stopping method.

So, the impulse in both the cases will be same.