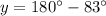Question

1. In triangle XYZ, A is the midpoint of XY, B is the midpoint of YZ, and C is the midpoint of XZ. Also, AY = 7, BZ = 8, and XZ = 18. What is the perimeter of triangle ABC? (SHOW WORK)

2. What is y? (SHOW WORK) 2nd picture is the triangle.

Answer 1

Part 1) The perimeter of triangle ABC is 24 units

Part 2)
`y=97\°`

Explanation:

Part 1) we know that

The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

see the attached figure to better understand the problem

so

Applying the midpoint theorem

step 1

Find the value of BC

`BC=(1)/(2)XY`

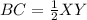
`XY=2AY` ---> because A is the midpoint

substitute the given value of AY

`XY=2(7)=14\ units`

`BC=(1)/(2)(14)=7\ units`

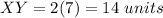
step 2

Find the value of AC

`AC=(1)/(2)YZ`

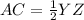
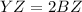`YZ=2BZ` ---> because B is the midpoint

substitute the given value of BZ

`YZ=2(8)=16\ units`

`AC=(1)/(2)(16)=8\ units`

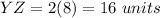
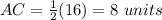
step 3

Find the value of AB

`AB=(1)/(2)XZ`

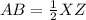
substitute the given value of XZ

`AB=(1)/(2)(18)=9\ units`

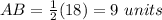
step 4

Find the perimeter of triangle ABC

`P=AB+BC+AC`

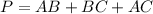
substitute

`P=9+7+8=24\ units`

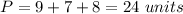
Part 2) Find the measure of angle y

step 1

Find the measure of angle z

we know that

The sum of the interior angles in a triangle must be equal to 180 degrees

so

`55\°+42\°+z=180\°`

solve for z

`97\°+z=180\°`

`z=180\°-97\°`

`z=83\°`

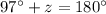
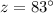
step 2

Find the measure of angle y

we know that

`z+y=180\°` ----> by supplementary angles (form a linear pair)

we have

`z=83\°`

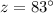
substitute

`83\°+y=180\°`

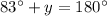
solve for y

`y=180\°-83\°`

`y=97\°`