Question

A 670.-g piece of copper tubing is heated to 95.3°C and placed in an insulated vessel containing 52.5 g of water at 36.5°C. Assuming no loss of water and heat capacity of 10.0 J/K for the vessel, what is the final temperature (c of copper = 0.387 J/g · K)?

Answer 1

Final temperature will be T = 67.68°C

Step-by-step explanation:

The heat evolved by the copper tubing will be absrobed by both water and the vessel used.

The heat evolved by the copper tubing will be:

Heat =
`Q1=massXspecificheatX(changeintemperature)`

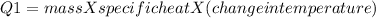
Mass = 670 g

Specific heat = 0.387 J/g · K

Change in temperature = Initial - Final

`Q1=670X0.387X(ChangeinTemperature)`

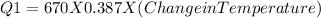
The heat absorbed by water will be

`Q2=massXspecificheatXchangeintemperature`

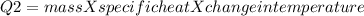
mass = 52.5

Specific heat = 4.184 J/g · K

the heat absorbed by vessel will be:

`Q3=heatcapacityXchange intemperature`

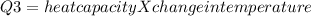
Heat capacity = 10J/K

Final temperature of all the three will be same (say T)

`Q1=Q2+Q3`

`670X0.387X(ChangeinTemperature)=massXspecificheatXchangeintemperature+heatcapacityXchange intemperature`

`670X0.387X(95.3-T)=(52.5X4.184X(T-36.5))+(10X(T-36.5)`

`259.29(95.3-T)=219.66(T-36.5)+10(T-36.5)`

`24710.337-259.29T=219.66T-8017.59+10T-365`

`33092.59=488.95T`

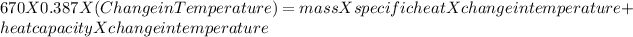
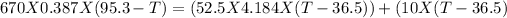
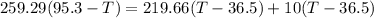
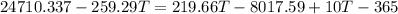
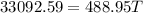
T = 67.68°C