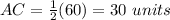Answer:

Explanation:
The correct question is
A, B, and C are midpoints of ∆XYZ. What is the length of XY
we know that
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side
step 1
Find the length of YZ
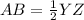
we have

substitute
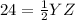
solve for YZ
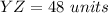
step 2
Find the length of XY
Applying Pythagoras Theorem in the right triangle XYZ
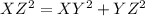
substitute the given values
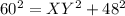
solve for XY
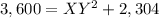

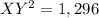

Applying the Midpoint Theorem
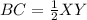 ----->
----->
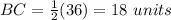
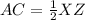 ----->
----->