Question

If a fair coin is flipped 15 times, what is the probability that there are more heads than tails?

Answer 1

Explanation:

Answer 2

The probability that there are more heads than tails is equal to
`(1)/(2)`.

Explanation:

Since the number of flips is an odd number, there can't be an equal number of heads and tails. In other words, there are either

• more tails than heads, or,
• more heads than tails.

Let the event that there are more heads than tails be
`A`.
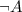`\lnot A` (i.e., not A) denotes that there are more tails than heads. Either one of these two cases must happen. As a result,
`P(A) + P(\lnot A) = 1`.

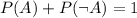Additionally, since this coin is fair, the probability of getting a head is equal to the probability of getting a tail on each toss. That implies that (for example)

• the probability of getting 7 heads out of 15 tosses will be the same as
• the probability of getting 7 tails out of 15 tosses.

Due to this symmetry,

• the probability of getting more heads than tails (A is true) is equal to
• the probability of getting more tails than heads (A is not true.)

In other words
`P(A) = P(\lnot A)`.

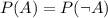Combining the two equations:

`\left\{\begin{aligned}&P(A) + P(\lnot A) = 1 \cr &P(A) = P(\lnot A)\end{aligned}\right.`,

`P(A) = P(\lnot A) = (1)/(2)`.

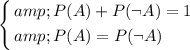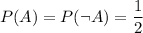In other words, the probability that there are more heads than tails is equal to
`(1)/(2)`.

This conclusion can be verified using the cumulative probability function for binomial distributions with
`(1)/(2)` as the probability of success.

`\begin{aligned}P(A) =& P(n \ge 8) \cr =& \sum \limits_(i = 8)^(15) {15 \choose i} (0.5)^(i) (0.5)^(15 - i)\cr =& \sum \limits_(i = 8)^(15) {15 \choose i} (0.5)^(15)\cr =& (0.5)^(15) \left({15 \choose 8} + {15 \choose 9} + \cdots + {15 \choose 15}\right) \cr =& (0.5)^(15) \left({15 \choose (15 - 8)} + {15 \choose (15 - 9)} + \cdots + {15 \choose (15 - 15)} \right) \cr =& (0.5)^(15) \left({15 \choose 7} + {15 \choose 6} + \cdots + {15 \choose 0}\right)\end{aligned}`

`\begin{aligned}\phantom{P(A)} =& \sum \limits_(i = 0)^(7) {15 \choose i} (0.5)^(15)\cr =& P(n \le 7) \cr =& P(\lnot A)\end{aligned}`.