Question

A cord is wrapped around the rim of a solid uniform wheel 0.280m in radius and of mass 8.80kg. A steady horizontal pull of 32N to the right is exerted on the cord, pulling it off tangentially from the wheel. The wheel is mounted on frictionless bearings on a horizontal axle through its center. What is the wheels angular acceleration? What force does the axle apply to the wheel? What torque does the axle apply to the wheel?

Answer 1

Answer:
`25.97 rad/s^2`

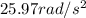
Step-by-step explanation:

Given

radius of wheel
`r=0.28 m`

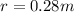
mass of wheel
`m=8.80 kg`

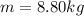
Force
`F=32 N`

Moment of Inertia of solid wheel
`I=(mr^2)/(2)`

`I=(8.8* 0.28^2)/(2)`

`I=0.344 kg-m^2`

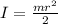
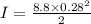
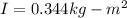
Torque is given by

`\tau =F* r=I* \alpha`

`32* 0.28=0.344* \alpha`

`\alpha =25.97 rad/s^2`

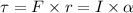
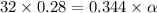
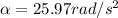
Force on the axle is 32 N since there is no linear acceleration of the system

using Third law F=32 N

Torque of the axle applied to the wheel is zero because force of axle imparted at the center of axle