Question

A sample of 16 items provides a sample standard deviation of 9.5. Test the following hypotheses using α = .05.Η 0 : σ 2 ≤ 50Η a : σ 2 > 50Calculate the value of the test statistic (to 2 decimals).The p-value isless than .01 between .01 and .025 between .025 and .05 between .05 and .01 between .05 and .10 greater than .10Item 2What is your conclusion?Conclude that the population variance is greater than 50Cannot conclude that the population variance is greater than 50Repeat the hypothesis test using the critical value approach.What is the rejection rule for this hypothesis test?Reject Η 0 if χ 2greater than greater than or equal to less than or equal to less thanWhat is your conclusion?Conclude that the population variance is greater than 50 Cannot conclude that the population variance is greater than 50

Answer 1

The p-value is between .025 and .05

p-value = 0.028

The critical region is χ² ≥ 24.996

Using both approaches the decision is to reject the null hypothesis.

Explanation:

Hello!

You have the following hypothesis

H₀: σ² ≤ 50

H₁: σ² > 50

α: 0.05

To test the population variance, the statistic to use has is Chi-Square distribution:

χ²= (n-1)S² ~χ²
`_(n-1)`

σ²

With n= 16 and S= 9.5

The statistic value is:

χ²= (16-1)(9.5)² = 27.075

50²

This is a one-tailed test, to calculate the p-value you have to calculate the probability of the χ² value.

P(χ²
`_(15)` ≥ 27.075) = 1 - P(χ²
`_(15)` < 27.075) = 1 - 0.972 = 0.028

The p-value is between .025 and .05

p-value = 0.028

Since the p-value ≤ α the decision is to reject the null hypothesis. You can conclude that the population variance is greater than 50.

As I said this is a one-tailed test, the critical value is:

χ²
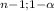`_(n-1; 1-\alpha )` = χ²
`_(15;0.95)` = 24.996

Decision:

If χ² ≥ 24.996 then you reject the null hypothesis.

If χ² < 24.996 then you support the null hypothesis.

Since the calculated χ² value is greater than the critical value, you reject the null hypothesis.

I hope you have a SUPER day!