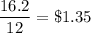Question

A local sorority sold hot dogs and bratwursts at the spring fling picnics. The first day they sold 8 dozen hot dogs and 13 dozen bratwursts for $316.20.The second day they sold 10 dozen hot dogs and 15 dozen bratwursts for a total of $375.00. How much did each​ cost? Solve this system using an inverse matrix.​ (Hint: It's easier to leave the dozens in the problem until the last​ step.)

Answer 1

Answer: Cost of each hot dog and bratwursts would be $1.1 and $1.35 each.

Explanation:

Since we have given that

Cost of each dozen hot dogs be 'x'.

Cost of each dozen bratwursts be 'y'.

The first day they sold 8 dozen hot dogs and 13 dozen bratwursts for $316.20.

So, the equation would be

`8x+13y=\$316.20`

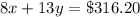
.The second day they sold 10 dozen hot dogs and 15 dozen bratwursts for a total of $375.00.

So, the equation would be

`10x+15y=\$375.00\\\\2x+3y=\$75`

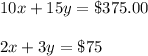
So, the equations becomes

`8x+13y=316.20--------------(2)\\\\(2x+3y=75)* 4\\\\\implies 8x+12y=300------------(1)`

So, by elimination method, we get that

`8x+13y=316.20\\\\(-)8x+(-)12y=(-)300\\\\--------------\\y=\$16.20`

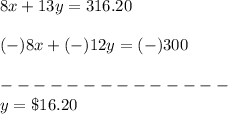
Put the value of y in the eq(1), we get that

`2x+3y=75\\\\2x+3(16.20)=75\\\\2x+48.6=75\\\\2x=75-48.60\\\\2x=26.4\\\\x=(26.4)/(2)\\\\x=\$13.2`

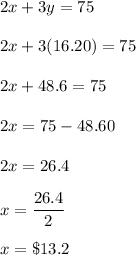
Hence, the cost of hot dogs would be
`(13.2)/(12)=\$1.1`

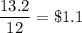
And the cost of bratwursts would be
`(16.2)/(12)=\$1.35`