Question

25 point for this question:

For which values of a and b the following is true for any real number x?

Answer 1

The values of a and b are
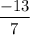`$ (-13)/(7) $` and
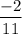`$ (-2)/(11) $` respectively.

Explanation:

Given that
`$ (x - 4)/(x^2 + 7x - 18) = (a)/(x + 9) + (b)/(x - 2) $`

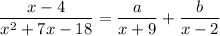
We solve this by partial fraction method.

Taking L.C.M. in the RHS, we get

`$ (x - 4)/(x^2 + 7x - 18) = (a(x - 2) + b(x + 9))/((x + 9)(x - 2)) $`

`$ \implies x - 4 = a(x - 2) + b(x + 9) $`

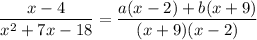
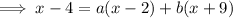
To find the value of 'b', substitute x = 2. This would make 'a' vanish leaving an equation with 'b'.

Therefore, 2 - 4 = a(2 - 2) + b(2 + 9)

⇒ -2 = 0 + b(11)

`$ \implies b = (-2)/(11) $`

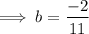
Similarly, substitute x = -9 to find the value of 'a'.

⇒ -9 - 4 = a(7) + b(0)

`$ \implies a = (-13)/(7) $`.

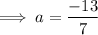Therefore, the values of 'a' and 'b'b are: =-13/7 and -2/11 respectively.