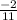Answer:
a=
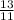 b =
b =
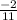
Explanation:
- By equating coefficients on both sides of respective terms.
Given,
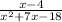 =
=
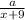 +
+
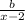
Now take lcm on right hand side
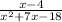 =
=
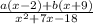
By equating coefficients of respective terms
x-4 = a(x-2)+b(x+9)
a+b=1 -----1 ; 9b-2a=-4 -----2
Substitute b=1-a in 2
9(1-a)-2a=-4
11a=9+4=13
a=
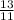
As b=1-a=1-
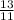 =
=