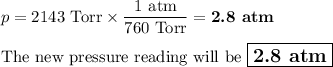Answer:

Step-by-step explanation:
The volume and amount are constant, so we can use Gay-Lussac’s Law:
At constant volume, the pressure exerted by a gas is directly proportional to its temperature.
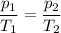
Data:
p₁ = 1520 Torr; T₁ = 27 °C
p₂ = ?; T₂ = 150 °C
Calculations:
(a) Convert the temperatures to kelvins
T₁ = ( 27 + 273.15) K = 300.15 K
T₂ = (150 + 273.15) K = 423.15 K
(b) Calculate the new pressure
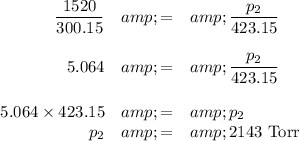
(c) Convert the pressure to atmospheres