To develop this problem, it is necessary to apply the concepts related to the description of the movement through the kinematic trajectory equations, which include displacement, velocity and acceleration.
The trajectory equation from the motion kinematic equations is given by

Where,
a = acceleration
t = time
 = Initial velocity
= Initial velocity
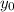 = initial position
= initial position
In addition to this we know that speed, speed is the change of position in relation to time. So

x = Displacement
t = time
With the data we have we can find the time as well

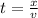


With the equation of motion and considering that we have no initial position, that the initial velocity is also zero then and that the acceleration is gravity,

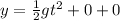
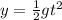


Therefore the vertical distance that the ball drops as it moves from the pitcher to the catcher is 1.46m.