Answer:
22.5
Explanation:
The region R contains every point of the plane with coordinate x between 3 and 9, and with coordinate y positive such that y < f(x) and y < g(x).
We can note that both f and g are positive on [3,9] because g is a decreasing linear function and g(9) = 0, thus g is positive in every other point of the interval, and f(x) = (x-3)^2 is always positive excpept when x = 3, where it reaches the value 0.
The interception of the graphs takes place for a value x such that f(x) = g(x).
We compute x^2-6x+9 = -3x + 27, thus x^2-6x+9-(-3x + 27) = x^2-3x -18 = 0.
The roots of that quadratic function are
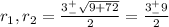 , thus r1 = 6, r2 = -3. We dont care about -3 because it is outside the interval, but we know that f and g graphs intersects on x = 6. Thus, we obtain, due to Bolzano Theorem:
, thus r1 = 6, r2 = -3. We dont care about -3 because it is outside the interval, but we know that f and g graphs intersects on x = 6. Thus, we obtain, due to Bolzano Theorem:
- On the interval [3,6), the function f in smaller because it takes the value 0 on x=3, while g is always positive.
- On the interval (6,9]. the function g is smaller because it takes the value 0 on x=9, while f is always positive
Hence, the upper bound is f on the interval [3,6) and g on the interval (6,9]. While the lower bound is the 0 function.
We need to calculate the following integral, using Barrow's rule
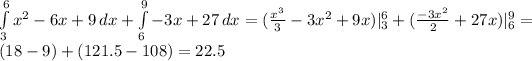
As a result, the area of the region R is 22.5