Answer:
b)
i) Cost: 342491.10 dollars
Average cost: 342.49 dollars per unit
Marginal cost: 389.73 dollars
ii) The average cost is minimized with 400 units
iii) The minimun average cost is 320 dollars per unit
Explanation:
a) If the average cost reaches a minimun when the amount of units is x, then c'(x) = 0. Using the division rule, we can calculate the derivate of c(x) in terms of the derivate of C(x).
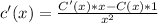
c'(x) = 0 when the numerator is 0, therefore C'(x)*x - C(x) = 0. After a simple calculation, we conclude that
 , in other words, the marginal cost equals the average cost when the average cost is minimun. That proves (a).
, in other words, the marginal cost equals the average cost when the average cost is minimun. That proves (a).
b)
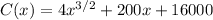
i) The cost, in dollars, is calculated by evaluating C in 1000
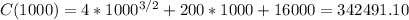
the average cost, in dollars per unit produced, c(1000), is obtained by dividing C(1000) by 1000

In order to calculate the marginal cost, we first derivate C(x):
C'(x) = 4*(3/2) * x^{1/2} + 200 = 6√x + 200
Then, we evaluate the derivate on 1000: C'(1000) = 6√1000 + 200 = 389.73
ii) We need to minimaze c(x) = C(x)/x. Using the item (a), we have to calculate x such that C(x)/x = C'(x), or, equivalently h(x) = C'(x)*x-C(x) = 0.
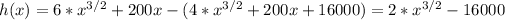
We obtain that h(x) = 0, only when
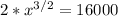 , thus,
, thus,
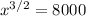 . Therefore
. Therefore
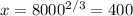 . We conclude that the production level that will minimize the average cost is 400 units.
. We conclude that the production level that will minimize the average cost is 400 units.
iii) The minimun average cost (in dollars per unit) is obtained by evaluating c(x) on 400, which is the value that minimizes the average cost (computed on the previous item). c(400) = C(400)/400 = (16000+200*400+4*400^(3/2))/400 = 40+200+4*√400 = 320.