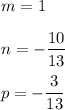Answer:
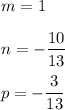
Explanation:
Given
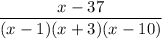
Rewrite it in the form
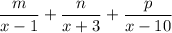
To find
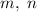 and
and
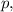 add these three fractions:
add these three fractions:

This fraction and initial fraction are equal, they have the same denominators, so they have the same numerators:

Equate coefficients:
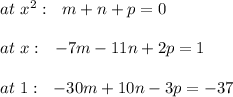
from the first equation:
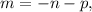
then
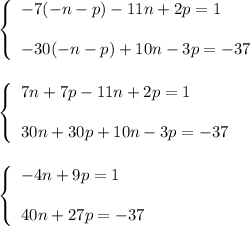
Multiply the first equation by 10 and add it to the second equation:

Then

Hence,
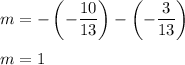
So,