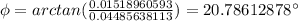Question

A 100 Ω resistor is connected in series with a 47 µF capacitor and a source whose maximum voltage is 5 V, operating at 100.0 Hz. Find the following. • The capacitive reactance of the circuit • The impedance of the circuit • The maximum current in the circuit • The phase angle

Answer 1

`X_c=-33.86275385\Omega`

`|Z|=105.5778675\Omega`

`I=0.04735841062A`

`\phi=20.78612878\°`

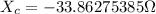
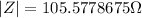
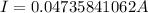
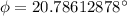
Step-by-step explanation:

The electrical reactance is defined as:

`X_c=-(1)/(2\pi fC)`

Where:

`f=Frequency\\C=Capacitance`

So, replacing the data provided by the problem:

`X_c=(1)/(2\pi *100*(47*10^(-6) )) =-33.86275385\Omega`

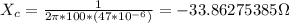
Now, the impedance can be calculated as:

`Z=R+jX_c`

Where:

`R=Resistance\\X_c= Capacitive\hspace{3}reactance`

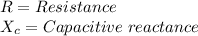
Replacing the data:

`Z=100-j33.86275385`

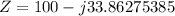
In order to find the magnitude of the impedance we can use the next equation:

`|Z|=√((R^2)+(X_c^2))=√((100)^2+(-33.86275385)^2) =105.5778675\Omega`

We can use Ohm's law to find the current:

`V=I*Z\\I=(V)/(Z)`

Therefore the current is:

`I=(5)/(100-j33.86275385)=0.04485638113+0.01518960593j`

And its magnitude is:

`|I|=√((0.04485638113)^2+(0.01518960593)^2) =0.04735841062\Omega`

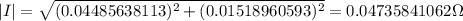
Finally the phase angle of the current is given by:

`\phi=arctan((0.01518960593)/(0.04485638113))=20.78612878\°`