Answer:
-1.1
Step-by-step explanation:
Data provided in the question:
Average temperature is rising at a rate,
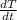 = 0.15°C/year
= 0.15°C/year
Rate of change rainfall,
 = - 0.1 cm/year
= - 0.1 cm/year
 = -2
= -2
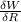 = 8
= 8
Now,
we need to calculate

since,
The wheat production (W) is dependent on the rainfall (R) and the Temperature (T)
thus, Using the chain rule , we have
 =
=
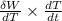 +
+
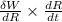
on substituting the respective values, we get
 = -2 × 0.15 + 8 × (-0.1)
= -2 × 0.15 + 8 × (-0.1)
or
 = -0.3 - 0.8
= -0.3 - 0.8
or
 = -1.1
= -1.1