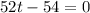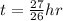Question

Two bicycles are traveling along perpendicular roads. Bicycle A is traveling due east at 4 mi/hr, and bicycle B is travelling due north at 6 mi/hr. At noon, when bicycle A reaches the intersection, bicycle B is 9 mi away and moving toward the same intersection If t is the number of hours after noon, the bicycles are closest together when t isA. 0B. 27/26C. 9/5D. 3/2E. 14/13

Answer 1

Explanation:

Given

speed of cyclist A is
`v_a=4 mi/hr`

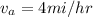
speed of cyclist B is
`v_b=6 mi/hr`

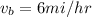
At noon cyclist B is 9 mi away

after noon Cyclist B will travel a distance of 6 t and cyclist A travel 4 t miles in t hr

Now distance of cyclist B from intersection is 9-6t

Distance of cyclist A from intersection is 4 t

let distance between them be z

`z^2=(9-6t)^2+(4t)^2`

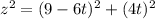
Differentiate z w.r.t time

`2z\frac{\mathrm{d} z}{\mathrm{d} t}=2* (9-6t)* (-6)+2* (4t)* 4`

`z\frac{\mathrm{d} z}{\mathrm{d} t}=(-6)(9-6t)+4(4t)`

`\frac{\mathrm{d} z}{\mathrm{d} t}=(16t+36t-54)/(z)`

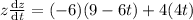
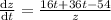
Put
`\frac{\mathrm{d} z}{\mathrm{d} t}\ to\ get\ maximum\ value\ of\ z`

therefore
`52t-54=0`

`t=(54)/(52)`

`t=(27)/(26) hr`