Answer:
a)
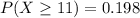
b)
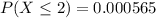
c) Mean = 8.8
Explanation:
1) Previous concepts
Binomial Distribution is a "discrete probability distribution which is used to calculate the probabilities for the independent trials and for each trial there is only two outcomes success or failure and probability for each success remains constant throughout each trial".
The Binomial distribution is a type of Bernoulli experiment with following properties:
a)There are two possible outcomes; success or failure.
b) Outcomes are independent on preceding result of a trial.
c) The probability of success remains constant throughout the experiment.
d)The number of successes are fixed.
The probability mass function for the Binomial distribution is given by:
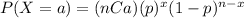
Where
 is the probability of success, n the number of trials and x the number of successes that we want on the n trials.
is the probability of success, n the number of trials and x the number of successes that we want on the n trials.
 represent the number federal inmates that are serving time for drug dealing
represent the number federal inmates that are serving time for drug dealing
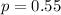 represent the proportion of federal inmates that are serving time for drug dealing
represent the proportion of federal inmates that are serving time for drug dealing
 random sample selected
random sample selected
2) Part a
The random variable X follows this distribution
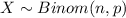
On this case we want the following probability, and since says greater or equal than 11 we can express like this:
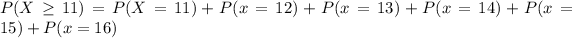
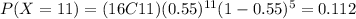
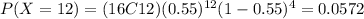

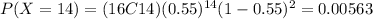
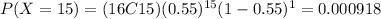
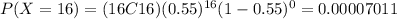
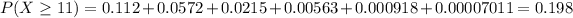
3) Part b
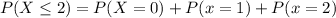


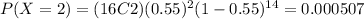
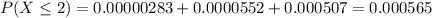
4) Part c
The expected value for the binomial distribution is given by the following formula:

So then the average number of federal inmates that are serving time for drug dealing on a sample of 16 is approximately 9.