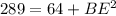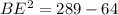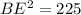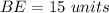Question

The quadrilateral shown is a rhombus. If AB = 17 and AE = 8, what is the measure of BE

Answer 1

C) 16

Explanation:

Answer 2

`BE=15\ units`

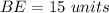
Explanation:

we know that

In a rhombus the diagonals are perpendicular

so

The triangle ABE is a right triangle

see the attached figure to better understand the problem

Applying the Pythagoras Theorem to the right triangle ABE

`AB^2=AE^2+BE^2`

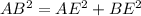
where

AB is the hypotenuse of the right triangle (greater side)

AE and BE are the legs of the right triangle

we have

`AB=17\ units\\AE=8\ units`

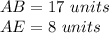
substitute

`17^2=8^2+BE^2`

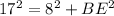
solve for BE

`289=64+BE^2`

`BE^2=289-64`

`BE^2=225`

`BE=15\ units`