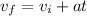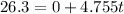Answer:
Part a)
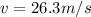
Part b)

Step-by-step explanation:
As we know that there is no friction on the hill
so here by energy conservation we will have

so we will have

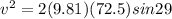
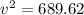
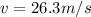
now in order to find the time we know that the acceleration along the surface is given as
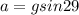
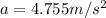
now we have