Question

The 488 nm line from an argon ion laser is Doppler broadened to 2.7×109 Hz. Given that the laser’s mirrors are 1 m apart, determine the number of longitudinal modes within the gain bandwidth of the 488 nm line. Assume that the index of refraction of the gas is 1

Answer 1

The number of longitudinal modes within the gain bandwidth is 18.

Step-by-step explanation:

Given that,

Wavelength = 488 nm

Frequency
`f=2.7*10^(9)\ Hz`

Distance = 1 m

Index of refraction of the gas = 1

We need to calculate the number of longitudinal modes within the gain bandwidth

Using formula of number of longitudinal modes

`N=(f* 2*\mu* l)/(c)`

Where, f = Doppler frequency

c = speed of light

l= separation

Put the value into the formula

`N=(2.7*10^(9)**2*1*1)/(3*10^(8))`

`N=18`

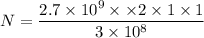
Hence, The number of longitudinal modes within the gain bandwidth is 18.