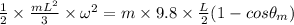Answer:
Maximum angle is
 rad
rad
Step-by-step explanation:
As per the question:
length of the pendulum, L = 0.30 m
Radius of the pendulum, R = 0.001 m
Angular speed at the bottom,

Now,
To calculate the maximum angle,
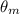 :
:
For the pendulum, the moment of inertia, I =
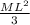
Now, using the principle of the conservation of energy:
Kinetic energy = Potential energy
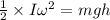
where
h =
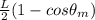
Thus