Question

Consider Rosenbrock’s Function f(x, y) = (1 − x) 2 + 100(y − x 2 ) 2 .

a) Using ad-hoc/elementary reasoning, identify a global min and argue that this min is unique.

b) Confirm that this function is not convex using a characterization of convexity (as opposed to the definition of convexity). Hint: Consider the point x y = −.1 .3 .

Answer 1

See steps below

Explanation:

The function

`\large f(x,y)=(1-x)^2+100(y-x^2)^2`

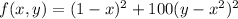
is a particular case of the general Rosenbrock’s Function.

a)

Since

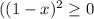`\large ((1-x)^2\geq 0` for all the values of x and equals 0 when x=1 and

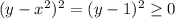`\large (y-x^2)^2=(y-1)^2\geq 0` for all the values of y and equals 0 only when y=1, we conclude that (1,1) is a minimum.

On the other hand,

f(x,y)>0 for (x,y) ≠ (1,1) so (1,1) is a global minimum.

b)

To confirm that this function is not convex, we will be using the following characterization of convexity

“f is convex if, and only if, the Laplace operator of f
`\large \\abla^2f \geq 0` for every (x,y) in the domain of f”

Given that the domain of f is the whole plane XY, in order to prove that f is not convex, we must find a point (x,y) at where the Laplace operator is < 0.

The Laplace operator is given by

`\large \\abla^2f=\displaystyle(\partial ^2f)/(\partial x^2)+\displaystyle(\partial ^2f)/(\partial y^2)`

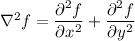
Let us compute the partial derivatives

`\large \displaystyle(\partial f)/(\partial x)=-2(1-x)+200(y-x^2)(-2x)=-2+2x-400xy+400x^3\\\\\displaystyle(\partial^2 f)/(\partial x^2)=2-400y+1200x^2`

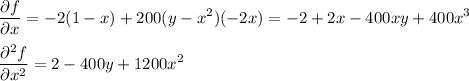
and

`\large \displaystyle(\partial f)/(\partial y)=200(y-x^2)=200y-200x^2\\\\\displaystyle(\partial^2 f)/(\partial x^2)=200`

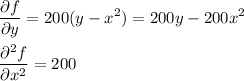
we have then

`\large \\abla^2 f=2-400y+1200x^2+200`

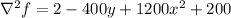
if we take (x,y) = (0,1)

`\large \\abla^2 f(0,1)=2-400+200=202-400=-198<0`

hence f is not convex.