Question

A model used for the yield Y of an agricultural crop as a function of the nitrogen level N in the soil ) (measured in appropriate units) is Y = (kN) / (1 + N2) where k is a positive constant. What nitrogen levels gives the best yield?

Answer 1

A nitrogen level of 1 gives the best yield.

Explanation:

We are given the following:

Yield Y of an agricultural crop as a function of the nitrogen level N in the soil

`Y(N) = \displaystyle(kN)/(1+N^2)`

First, we differentiate Y(N) with respect to N, to get,

`\displaystyle(d(Y(N)))/(dN) = \displaystyle(d)/(dN)\Bigg(\displaystyle(kN)/(1+N^2)\Bigg)\\\\= ((1+N^2)k-kN(2N))/((1+N^2)^2)\\\\=(k-kN^2)/((1+N^2)^2)`

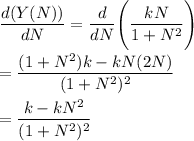
Equating the first derivative to zero, we get,

`\displaystyle(d(Y(N)))/(dN) = 0\\\\\Rightarrow (k-kN^2)/((1+N^2)^2) = 0`

Solving, we get,

`\displaystyle(k-kN^2)/((1+N^2)^2) = 0\\\\k-kN^2 = 0\\k(1-N^2) = 0\\k \\eq 0\\1-N^2 = 0\\N = \pm 1\\N \\eq -1\\N = 1`

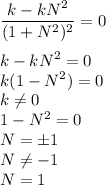
Again differentiation Y(N), with respect to N, we get,

`\displaystyle(d^2(Y(N)))/(dN^2) = \displaystyle(2kN(N^2-3))/((1+N^2)^3)`

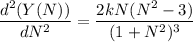
At N = 1

`(d^2(Y(N)))/(dN^2) < 0`

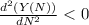
Thus, by double derivative test, the maximum value of Y(N) occurs at N = 1.

Thus, largest yield of crop is given by:

Y(1) =

`Y(N) = \displaystyle(k(1))/(1+(1)^2) = (k)/(2)`