Question

Suppose the Sunglasses Hut Company has a profit function given by P ( q ) = − 0.02 q 2 + 5 q − 30 , where q is the number of thousands of pairs of sunglasses sold and produced, and P ( q ) is the total profit, in thousands of dollars, from selling and producing q pairs of sunglasses.

Answer 1

A) Pairs of sunglasses should be sold to maximize profits is 100 thousand.

B) The actual maximum profits that can be expected is 180 thousands dollars.

Explanation:

Given : Suppose the Sunglasses Hut Company has a profit function given by
`P(q)=-0.02q^2+4q-20`

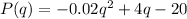
where, q is the number of thousands of pairs of sunglasses sold and produced and P(q) is the total profit, in thousands of dollars, from selling and producing q pairs of sunglasses.

To find :

A) How many pairs of sunglasses (in thousands) should be sold to maximize profits?

Profit is
`P(q)=-0.02q^2+4q-20`

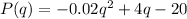
Compare with general quadratic equation
`ax^2+bx+c`

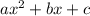
a=-0.02, b=4, c=-20

The maximum value of quadratic function is at
`x=-(b)/(2a)`

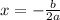
So, maximum profit occur at q is given by,

`q=-(4)/(2(-0.02))`

`q=(4)/(0.04)`

`q=100`

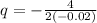
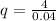
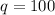
i.e. 100 thousand pair of sunglasses.

Pairs of sunglasses should be sold to maximize profits is 100 thousand.

B) What are the actual maximum profits (in thousands) that can be expected?

Maximum profit occurs at q=100 thousand pairs is given by,

`P(100)=-0.02(100)^2+4(100)-20`

`P(100)=-0.02* 10000+400-20`

`P(100)=180`

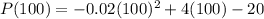
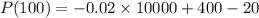
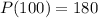
The actual maximum profits that can be expected is 180 thousands dollars.