Question

A survey was conducted that asked 1003 people how many books they had read in the past year. Results indicated that x overbar equals 12.8 books and sequels 16.6 books. Construct a 99​% confidence interval for the mean number of books people read. Interpret the interval.

Answer 1

The 99% confidence interval would be given (11.448;14.152).

Explanation:

1) Important concepts and notation

A confidence interval for a mean "gives us a range of plausible values for the population mean. If a confidence interval does not include a particular value, we can say that it is not likely that the particular value is the true population mean"

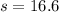`s=16.6` represent the sample deviation

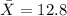`\bar X=12.8` represent the sample mean

n =1003 is the sample size selected

Confidence =99% or 0.99

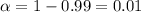`\alpha=1-0.99=0.01` represent the significance level.

2) Solution to the problem

The confidence interval for the mean would be given by this formula

`\bar X \pm z_(\alpha/2) (s)/(√(n))`

We can use a z quantile instead of t since the sample size is large enough.

For the 99% confidence interval the value of
`\alpha=1-0.99=0.01` and
`\alpha/2=0.005`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=2.58`

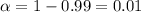And replacing into the confidence interval formula we got:

`12.8 - 2.58 (16.6)/(√(1003))=11.448`

`12.8 + 2.58 (16.6)/(√(1003)) =14.152`

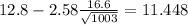
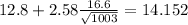
And the 99% confidence interval would be given (11.448;14.152).

We are confident that about 11 to 14 are the number of books that the people had read on the last year on average, at 1% of significance.