Question

Can someone help me with this problem? It’s Special Right Triangles: Decimal Answer. Round to the nearest tenth. Thank you ! 10 points

Answer 1

h = 1.4

c = 2.8

Explanation:

For each problem, remember the special triangle side ratios then use a proportion. To solve, isolate the variable.

For the triangle with the variable h:

Since two of the angles are 45, this is an isosceles triangle. All isosceles triangles have two equal sides that are not the hypotenuse.

In a right isosceles triangle, the ratio for regular side to hypotenuse is 1 to √2.

`(1)/(\sqrt2) =(h)/(2) \\h = 2(1)/(\sqrt2) \\h = (2)/(\sqrt2) \\h = (2\sqrt2)/(2) \\h = √(2)`

h = √2

h ≈ 1.4

For the triangle with the variable c:

The is an equilateral triangle cut in half because the angles are 30 and 60.

The side ratio of altitude to hypotenuse is √3 to 2.

`(√(3) )/(2) =(c)/(4) \\√(3) = (c)/(2)\\2\sqrt3 = c`

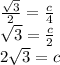
c = 2√2

c ≈ 2.8