Question

The attention span of little kids (ages 3–5) is claimed to be Normally distributed with a mean of 15 minutes and a standard deviation of 4 minutes. A test is to be performed to decide if the average attention span of these kids is really this short or if it is longer. You decide to test the hypotheses H0: μ = 15 versus Ha: μ > 15 at the 5% significance level. A sample of 10 children will watch a TV show they have never seen before, and the time until they walk away from the show will be recorded. If, in fact, the true mean attention span of these kids is 18 minutes, what is the probability of a Type II error?

Answer 1

P(Type ll error) = 0.2327

Explanation:

We are given the following in the question:

Population mean, μ = 15 minutes

Sample size, n = 10

Alpha, α = 0.05

Population standard deviation, σ = 4 minutes

First, we design the null and the alternate hypothesis

`H_(0): \mu = 18\\H_A: \mu > 18`

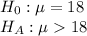
We use One-tailed z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

`z_(critical) \text{ at 0.05 level of significance } = 1.645`

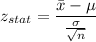
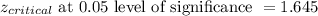
Putting the values, we get,

`z_(stat) = \displaystyle\frac{\bar{x}- 15}{(4)/(√(10)) } > 1.645\\\\\bar{x} -1 5 > 1.645* (4)/(√(10))\\\\\bar{x} -15 > 2.08\\\bar{x} = 17.08`

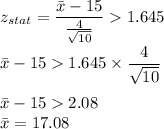
Type ll error is the error of accepting the null hypothesis when it is not true.

P(Type ll error)

`P(\bar{x}<17.07 \text{ when mean is 18})\\\\= P(z < \frac{\bar{x}-18}{(4)/(√(10))})\\\\= P(z < (17.08-18)/((4)/(√(10))))\\\\= P(z<-0.7273)`

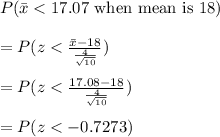
Calculating value from the z-table we have,

`P(z<-0.7273) = 0.2327`

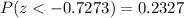
Thus,

P(Type ll error) = 0.2327