Question

Assume that all​ grade-point averages are to be standardized on a scale between 0 and 6. How many​ grade-point averages must be obtained so that the sample mean is within 0.01 of the population​ mean? Assume that a 98​% confidence level is desired. If using the range rule of​ thumb, sigma can be estimated as
`(r)/(4) = (6-0)/(4) = 1.5`. Does the sample size seem​ practical?

Answer 1

The sample size should be 122,150 and the sample size is not practical.

Explanation:

Consider the provided information.

The sample mean is within 0.01 of the population​ mean.

E=0.01

σ=1.5

Confidence level is 98​%

1-α=0.98

α=1-0.98=0.02

Formula for sample size is:
`n=((z_(\alpha/2)\sigma)/(E))^2`

By using the normal probability table:
`z_(\alpha/2)=z_(0.01)\approx2.33`

Substitute the respective values in the above formula.

`n=((2.33* 1.5)/(0.01))^2\approx122150`

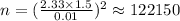
Sample size doesn't seem practical as 122,150 is extremely large number.