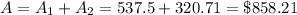Answer:
The amount would be $ 858.21
Explanation:
Given,
In first account,
Deposited amount,
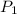 = $ 500,
= $ 500,
Annual simple interest,
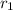 = 2.5%,
= 2.5%,
Number of years,
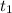 = 3 years,
= 3 years,
So, the amount after 3 years,
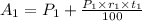
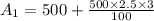

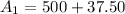

In second account,
Deposited amount,
 = $ 300,
= $ 300,
Annual compound interest,
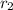 = 2.25%, ( ∵
= 2.25%, ( ∵
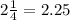 )
)
Number of years,
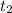 = 3 years,
= 3 years,
So, the amount after 3 years,
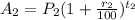
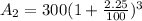
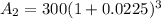
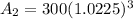

Hence, the total amount,