Question

If the absolute temperature of a gas is tripled, what happens to the root‑mean‑square speed of the molecules?

A. Nothing happens to the rms speed.
B. The new rms speed is 9 times the original rms speed.
C. The new rms speed is 3 times the original rms speed.
D. The new rms speed is 1.732 times the original rms speed.
E. The new rms speed is 1/3 the original rms speed.

Answer 1

D. The new rms speed is 1.732 times the original rms speed.

Step-by-step explanation:

The expression for the root mean square speed is:

`C_(rms)=\sqrt {\frac {3RT}{M}}`

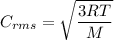
R is Gas constant having value = 8.314 J / K mol

M is the molar mass of gas

T is the absolute temperature

As seen from the formula, root mean square speed is directly proportional to the square root of the absolute temperature.

So,

`C_(rms)\propto \sqrt {T}`

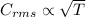
Given, absolute temperature of a gas is tripled, so, the new rms speed will be √3 (1.732) of the original.

Hence, the correct option is:- D. The new rms speed is 1.732 times the original rms speed.