Question

SAT scores are normally distributed with a mean of 1518 and standard deviation of 325. If 16 SAT scores are randomly selected, find the probability that they have a sample mean that is between 1440 and 1480, P(1440 < sample mean < 1480). Load the leading zero and round your answer to four decimal places.

Answer 1

The probability that the sample mean of 16 SAT scores falls between 1440 and 1480 is approximately 0.0471

Lets find the Z-scores:

Z1 = (1440 - 1518) / (325/√16) = -0.2400

Z2 = (1480 - 1518) / (325/√16) = -0.1169

Lets find Probability using Standard Normal Distribution:

P(1440 < Xbar < 1480) = P(-0.2400 < z < -0.1169)

Using the Z-Table, we can find the z-scores:

P(z < -0.2400) = 0.4051

P(z < -0.1169) = 0.4522

The Probability:

P(1440 < Xbar < 1480) = P(-0.2400 < z < -0.1169) = 0.4522 - 0.4051 = 0.0471

The probability that the sample mean of 16 SAT scores falls between 1440 and 1480 is approximately 0.0471

Answer 2

The probability that a random sample of 16 SAT scores has a sample mean between 1440 and 1480 is 0.1464

Explanation:

The probability that the sample mean is between 1440 and 1480 is equal to the probability that the sample mean is below 1480 minus the probability that the sample mean is below 1440, or

P(1440 < sample mean < 1480)

=P(sample mean<1480) - P(sample mean<1440)

To find these probabilities we need to calculate the statistic of 1440 and 1480, and it can be calculated as:

t=
`(X-M)/((s)/(√(N) ) )` where

• X is the sample mean (1440,1480)

• M is the mean SAT scores (1518)

• s is the standard deviation (325)

• N is the sample size (16)

then

t(1440)=
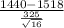`(1440-1518)/((325)/(√(16) ) )` =-0.96

t(1480)=
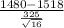`(1480-1518)/((325)/(√(16) ) )` = -0.4677

using the t table with 15 degrees of freedom we can find that

P(sample mean<1480) = P(t<-0.4677) = 0.3225

P(sample mean<1440) = P(t<-0.96) = 0.1761

Then P(1440 < sample mean < 1480) =0.3225 - 0.1761 = 0.1464