Question

In a random sample of 27 ​people, the mean commute time to work was 32.8 minutes and the standard deviation was 7.2 minutes. Assume the population is normally distributed and use a​ t-distribution to construct a 99 ​% confidence interval for the population mean mu . What is the margin of error of mu ​? Interpret the results.

The confidence interval for the population mean ___ , ___

​(Round to one decimal place as​ needed.)

A) Using the given sample​ statistics, find the left endpoint of the interval using​ technology, rounding to one decimal place.

B) Using the given sample​ statistics, find the right endpoint of the interval using​ technology, rounding to one deci?mal place.

C) Using the formulas and values for the left​ and/or right​endpoints, find the margin of error from​ technology, rounding to two decimal places.

Answer 1

A) Left endpoint of the interval = 28.9

B) Right endpoint of the interval = 36.7

C) Margin of error = 3.85

Explanation:

We are given the following in the question:

Sample size, n = 27

Sample mean = 32.8 minutes

Sample standard deviation = 7.2 minutes

The population is normally distributed.

99% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

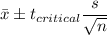
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 26 and}~\alpha_(0.01) = \pm 2.7787`

`32.8 \pm 2.7787(\displaystyle(7.2)/(√(27)) ) = 32.8 \pm 3.8502 = (28.9498 ,36.6502) \approx (28.9,36.7)`

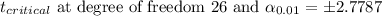
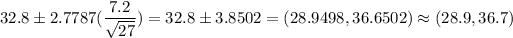
Margin of error =

`\displaystyle\frac{\text{Upper Interval-Lower Interval}}{2} = (36.65-28.95)/(2) = 3.85`

A) Left endpoint of the interval = 28.9

B) Right endpoint of the interval = 36.7

C) Margin of error = 3.85