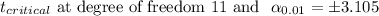Question

An important problem in industry is shipment damage. A windshield factory ships its product by truck and determines that it cannot meet its profit expectations if, on average, the number of damaged items per truckload is greater than 12. A random sample of 12 departing truckloads is selected at the delivery point and the average number of damaged items per truckload is calculated to be 9.4 with a calculated sample of variance of 0.64. Select a 99% confidence interval for the true mean of damaged items

a) [8.682, 10.12]
b) [39.48. -25.66]
c [11.28, 12.72]
d L-0.7181.0.7181
e) [8.707, 10.09
f) None of the above

Answer 1

Option A) (8.682, 10.12)

Explanation:

We are given the following in the question:

Sample mean,
`\bar{x}` = 9.4

Sample size, n = 12

Confidence level = 99%

Alpha, α = 0.01

Sample variance,
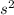`s^2` = 0.64

Sample standard deviation =
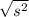`√(s^2)` = 0.8

Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

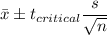
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 11 and }~\alpha_(0.01) = \pm 3.105`

`9.4 \pm 3.105(\displaystyle(0.8)/(√(12)) ) = 9.4 \pm 0.717 = (8.6829,10.1170) \approx (8.682,10.12)`