Question

1. Segment AE is 7 inches and AH is 7^/3 inches. What is the length of EH? Round to the nearest tenth.

7.0 inches
9.9 inches
12.1 inches
14.0 inches

2.The length of CD is 11 inches and the length of CF is 11^/3 inches. What is the length of DF? Round to the nearest tenth.
11 inches
15.6 inches
19.1 inches
22 inches

Answer 1

B

Explanation:

Answer 2

1.) 9.9

2.) 15.6

Explanation:

1.) Consider triangle AEH

AEH is a right angle triangle as ∠AEH = 90°

AH is the hypotenuse of the triangle.

Applying Pythagorean theorem

`AE^(2) + EH^(2) = AH^(2)`

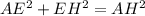
substituting values as given in the question:

`7^(2) +EH^(2)=(7√(3) )^(2)\\EH^(2)=(7√(3) )^(2)-7^(2) \\EH^(2)=98\\EH=√(98)\\EH=7√(2)`

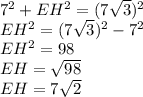
∴ EH≈9.9

2.) Consider triangle CDF

CDF is a right angle triangle as ∠CDF = 90°

CF is the hypotenuse of the triangle.

Applying Pythagorean theorem

`CD^(2) + DF^(2) = CF^(2)`

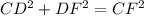
substituting values as given in the question:

`11^(2) +DF^(2)=(11√(3) )^(2)\\DF^(2)=(11√(3) )^(2)-11^(2) \\DF^(2)=242\\DF=√(242)\\DF=11√(2)`

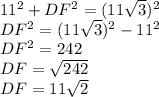
∴ DF≈15.6