Answer:
a. Z=0.8
b. 78.81%
Explanation:
The z-score for a woman measuring 'X' inches is given by:
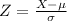
Where μ is the distribution mean and σ is the standard deviation.
Since each feet equals 12 inches, the woman's height is:
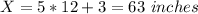
a. The z-score is:
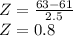
b. The percentage of women she is taller than can be found by checking for the corresponding percentile in a z-score table. A z-score of 0.8 is equivalent to the 78.81-th percentile. Therefore, she is taller than 78.81% of women.