An arch is 630 ft high and has 580=ft base. It can be modeled by the parabola =630\left [ 1-\left ( x/290 \right )^2 \right ]. Find the average height of the arch above the grou…

Question

asked Nov 15, 2020 223k views

1 Answer

Tomrlh · Answer 1 · 2020-11-19T13:35:12+0000

Answer:

420 ft

Explanation:

The given equation of a parabola is

$y=630[1-\left((x)/(290)\right)^(2)]$

An arch is 630 ft high and has 580=ft base.

Find zeroes of the given function.

y=0

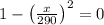
$630[1-\left((x)/(290)\right)^(2)]=0$

$1-\left((x)/(290)\right)^(2)=0$

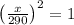
$\left((x)/(290)\right)^(2)=1$

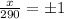
$(x)/(290)=\pm 1$

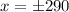
$x=\pm 290$

It means function is above the ground from -290 to 290.

Formula for the average height:

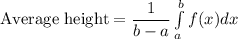
$\text{Average height}=(1)/(b-a)\int\limits^b_a f(x) dx$

where, a is lower limit and b is upper limit.

For the given problem a=-290 and b=290.

The average height of the arch is

$\text{Average height}=(1)/(290-(-290))\int\limits^(290)_(-290) 630[1-\left((x)/(290)\right)^(2)]dx$

$\text{Average height}=(630)/(580)[\int\limits^(290)_(-290) 1dx -\int\limits^(290)_(-290) \left((x)/(290)\right)^(2)dx]$

$\text{Average height}=(63)/(58)[[x]^(290)_(-290)-(1)/(84100)\left[(x^3)/(3)\right]^(290)_(-290)]$

Substitute the limits.

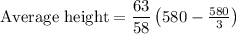
$\text{Average height}=(63)/(58)\left(580-(580)/(3)\right)$

$\text{Average height}=(63)/(58)((1160)/(3))$

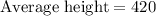
$\text{Average height}=420$

Therefore, the average height of the arch is 420 ft above the ground.