Question

Suppose that the strings on a violin are stretched with the same tension and each has the same length between its two fixed ends. The musical notes and corresponding fundamental frequencies of two of these strings are G (196 Hz) and E (659.3 Hz). The linear density of the E string is 3.40 × 10-4 kg/m. What is the linear density of the G string?

Answer 1

0.00384 kg/m

Step-by-step explanation:

The fundamental frequency of string waves is given by

`f=(1)/(2L)\sqrt{(F)/(\mu)}`

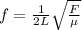
For some tension (F) and length (L)

`f\propto(1)/(\mu)`

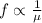
Fundamental frequency of G string

`f_G=196\ Hz`

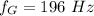
Fundamental frequency of E string

`f_E=659.3\ Hz`

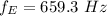
Linear mass density of E string is

`\mu_E=3.4* 10^(-4)\ kg/m`

So,

`(F_G)/(F_E)=\sqrt{(\mu_E)/(\mu_G)}\\\Rightarrow (F_G^2)/(F_E^2)=(\mu_E)/(\mu_G)\\\Rightarrow \mu_G=3.4* 10^(-4)* (659.3^2)/(196^2)\\\Rightarrow \mu_G=0.00384\ kg/m`

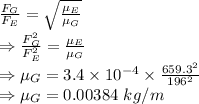
The linear density of the G string is 0.00384 kg/m