Question

0:0
3:1
6:2
9;3
is this direct variation or not?

Answer 1

Yes, the table represent a direct variation

Explanation:

we know that

A relationship between two variables, x, and y, represent a direct variation if it can be expressed in the form
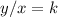`y/x=k` or
`y=kx`

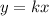
In a direct variation the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

In this problem , if the table represent a linear function, then the table represent a direct variation

Verify

For x=3, y=1

Find the value of the constant k of proportionality

`k=y/x` ---->
`k=1/3`

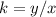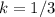
For x=6, y=2

Find the value of the constant k of proportionality

`k=y/x` ---->
`k=2/6=1/3`

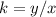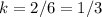
For x=9, y=3

Find the value of the constant k of proportionality

`k=y/x` ---->
`k=3/9=1/3`

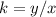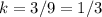
The values of k are equal

therefore

The table represent a direct variation