Question

Explain the difference between using the tangent ratio to solve for a missing angle in a right triangle versus using the cotangent ratio. You must use complete sentences and any evidence needed (such as an example) to prove your point of view. (10 points)

Answer 1

While determining the angle
`\theta` with the tangent ratio or cotangent ratio uses the same sides lengths but the ratios are inverse of each other.

Explanation:

See the diagram attached.

Let us assume a right triangle Δ ABC with ∠ B = 90°. Now, assume that the angle ∠ CAB =
`\theta` and the sides AB, BC, CA are 3, 4, 5 units respectively.

The tangent ratio of an angle
`\theta` is given by

`\tan \theta = (BC)/(AB) = (4)/(3)`

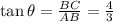
Again, the cotangent ratio of angle
`\theta` is given by

`\cot \theta = (AB)/(BC) = (3)/(4)`

Therefore, in both the cases of tangent ratio and cotangent ratio are inverse of each other and while determining the angle
`\theta` with the tangent ratio or cotangent ratio uses the same sides lengths but the ratios are inverse of each other. (Answer)