Question

Jerry solved this equation: 3 ( x − 1 4 ) = 13 6

1. 3x − 3 4 = 13 6
2. 3x − 3 4 + 3 4 = 13 6 + 3 4
3. 3x = 26 12 + 9 12
4. 3x = 35 12
5. ( 3 1 ) 3 1 x = 35 12 ( 3 1 )
6. x = 105 12
In which step did Jerry make an error?
A) In step 2, he should have subtracted 3/4 from both sides.
B) In step 3, he should have found an LCD of 10.
C) In step 4, he should have subtracted 9 from 26.
D) In step 5, he should have multiplied both sides by 1.3

Answer 1

D) In step 5, he should have multiplied both sides by 1/3

Explanation:

Given expression,

`3(x - (1)/(4)) = (13)/(6)`

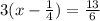
Using distributive property,

`3x - (3)/(4)=(13)/(6)`

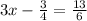
Using additive property of equality,

`3x -(3)/(4)+(3)/(4)=(13)/(6)+(3)/(4)`

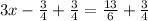
Make the fraction with same denominator by taking LCM of Denominators in left side the equation,

`3x = (26)/(12)+(9)/(12)`

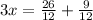
Adding fractions,

`3x =(35)/(12)`

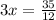
Write 3 as a fraction,

`(3)/(1)x =(35)/(12)`

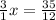
Using multiplicative property of equality for isolating the variable in right side, multiply 1/3 in both sides,

`x= (35)/(36)`

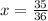
Hence, it is clear that he did mistake in step 5 he should have multiplied both sides by 1/3.