Answer:
0.0239
Explanation:
A publisher reports that 49% of their readers own a personal computer.
Claim : . A marketing executive wants to test the claim that the percentage is actually different from the reported percentage.
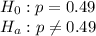
A random sample of 200 found that 42% of the readers owned a personal computer.
No. of people owned a personal computer =
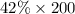
=

=
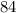
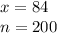
We will use one sample proportion test

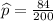
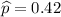
Formula of test statistic =
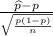
=
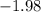
Now refer the p value from the z table
p value =0.0239
Hence The p value of test statistic is 0.0239