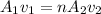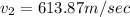Question

A garden hose having an internal diameter of 0.740 in. ( 1.8796 cm ) is connected to a lawn sprinkler that consists merely of an enclosure with 36 holes, each 0.055 in. ( 0.1397 cm ) in diameter. If the water in the hose has a speed of 4.00 ft/s ( 121.920 cm/s ), at what speed does it leave the sprinkler holes?

Answer 1

It will leave the sprinkler at speed of
`v_2=613.87m/sec`

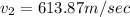
Explanation:

We have given internal diameter of the garden hose
`d_1=0.740in=1.8796cm`

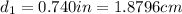
So radius
`r_1=(d_1)/(2)=(1.8796)/(2)=0.9398cm`

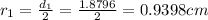
So area
`A_1=\pi r_1^2=3.14* 0.9398^2=2.7733cm^2`

Water in the hose has a speed of 4 ft/sec

So
`v_1=4ft/sec=121.92cm/sec(As\ 1ft/sec\ =30.48cm/sec)`

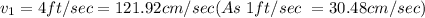
Number of holes n = 36

Diameter of each hole
`d_2=0.1397cm`

So radius
`r_2=0.0698cm`

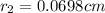
So area
`A_2=\pi r^2=3.14* 0.0698^2=0.0153cm^2`

From continuity equation

`A_1v_1=nA_2v_2`

`2.7733* 121.92=36* 0.0153* v_2`

`v_2=613.87m/sec`