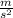Question

A1 kg-body moves upwards across the vertical wall due to the force F= 20 N applied at the angle a30° with vertical. Find the acceleration of the body if the coefficient of friction is k 0.05

Answer 1

The acceleration of the body is 7.0105
`(m)/(s^(2) )`

Step-by-step explanation:

From the free body diagram of the given case

Vertical component of the applied force ,
`F_(v)` = F cos(30°) =
`(√(3)F )/(2)` = 10
`√(3)`

Horizontal component of the applied force ,
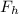`F_(h)` = F sin(30°)

Balancing the normal force(N) from the wall and
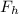`F_(h)` in horizontal direction.

N =
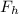`F_(h)` = F sin(30°) =
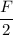`(F)/(2)` = 10 N

∵ The body is accelerating in vertical direction , the friction force acting on the body should be maximum.

∴ Maximum frictional force , f = k×N = 0.05×10 = 0.5 N

Let 'm' be the mass of the body and 'a' be the acceleration of the body in vertical direction and 'g' be the acceleration due to gravity.

∵ Body is accelerating in vertical direction , By Newton's 2nd law

`F_(v)` - f - mg= ma

∴ 10
`√(3)` - 0.5 - (1×9.81) = 1×a

∴ a = 7.0105
`(m)/(s^(2) )`