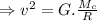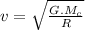Question

The equation for the speed of a satellite in a circular orbit around the Earth depends on mass. Which mass? The equation for the speed of a satellite in a circular orbit around the Earth depends on mass. Which mass? The mass of the satellite The mass of the sun The mass of the Earth

Answer 1

`v=\sqrt{(G.M_c)/(R) }`

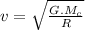
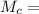`M_c=` mass of the earth.

Step-by-step explanation:

During the revolution of a satellite around a central mass of heavenly body:

`F_c=F_G`

`M_s.(v^2)/(R) =G.(M_s.M_c)/(R^2)`

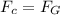
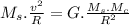
where:

G = gravitational constant

R = radius of the orbit

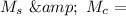`M_s\ \&\ M_c=`mass of satellite and mass of central heavenly body (here we've the Earth)

v = orbital speed of the satellite

`\Rightarrow v^2=G.(M_c)/(R)`

`v=\sqrt{(G.M_c)/(R) }`