Question

Assume that the number of bacteria follows an exponential growth model: P(t)=P0ektP(t)=P0ekt. The count in the bacteria culture was 800 after 10 minutes and 2000 after 30 minutes.

(a) What was the initial size of the culture?
(b) Find the population after 75 minutes.
(c) How many minutes after the start of the experiment will the population reach 11000?

Answer 1

a) The initial size is 506.

b) The population after 75 minutes is 24825.

c) 57 minutes after the start of the experiment will the population reach 11000.

Explanation:

Given : Assume that the number of bacteria follows an exponential growth model :
`P(t)=P_0e^(kt)`

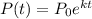
The count in the bacteria culture was 800 after 10 minutes and 2000 after 30 minutes.

According to information, we can find value of k

P(t)=2000,
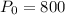`P_0=800` and t=30-10=20 minute

Substitute value in the model,

`2000=800* e^(k* 20)`

`(2000)/(800)=e^(20k)`

`2.5=e^(20k)`

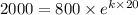
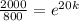
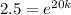
Taking ln both side,

`\ln(2.5)=\ln e^(20k)`

`\ln(2.5)=20k`

`k=(\ln(2.5))/(20)`

`k=0.0458`

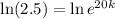
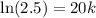
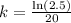
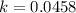
The model became
`P(t)=P_0e^(0.0458t)`

a) What was the initial size of the culture?

The count in the bacteria culture was 800 after 10 minutes.

So,
`800=P_0e^(0.0458* 10)`

`P_0=(800)/(e^(0.458))`

`P_0=506.03`

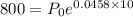
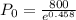
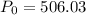
Approximately, the initial size is 506.

b) Find the population after 75 minutes.

So,
`P(75)=800* e^(0.0458* 75)`

`P(75)=800* e^(3.435)`

`P(75)=24825.13`

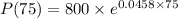
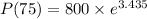
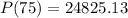
Approximately, the population after 75 minutes is 24825.

(c) How many minutes after the start of the experiment will the population reach 11000?

Here, P(t)=11000,
`P_0=800`

`11000=800* e^(0.0458* t)`

`(11000)/(800)=e^(0.0458* t)`

`13.75=e^(0.0458t)`

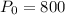
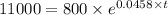
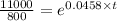
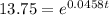
Taking natural log both side,

`\ln 13.75=\ln e^(0.0458t)`

`\ln 13.75=0.0458t`

`t=(\ln 13.75)/(0.0458)`

`t=57.22`

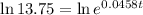
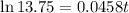
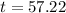
Approximately, 57 minutes after the start of the experiment will the population reach 11000.